what mosquitoes taught me about algorithm design

posted apr 2025, reprised from a fun unserious talk I first gave in jul 2024¹

Every Singaporean Son spends 2 years after high school doing something random of some mysterious force’s choosing. I think a plurality of people do some flavour of bashing through a forest with assault rifles, but I was somehow assigned² “preventive medicine” and “biodefence”, which turned out to be a euphemism for “an assortment of mosquito work”.

This is real — here’s a public Facebook post from the Ministry of Defence about us conscripts who, among other things, sit in a lab and morphologically identify mosquitoes through a microscope.

---

So, how does one identify a mosquito? You use a taxonomic key, of which the most established type is known as a dichotomous key. Basically, some mosquito expert has written a list of “yes/no” questions where at each step, you either land on a species that you trace through until you reach a species name. The “state of the art” keys³ I’d refer to looked like this:

With the deep arcane wisdom that 18-year-old-me wielded from half-listening in high school CS classes, I thought:

> Our dichotomous key looks like a right-skew binary tree. A traversal of a right-skew binary tree takes O(N) time (that is, in the worst case, you’d have to go through every species in the key).

> If we can somehow turn it into a balanced binary tree, we could get the time complexity of a traversal down to O(log N)!!

> smaller Big O -> faster mosquito identification -> I get more free time yay

So I did just that! I spent ~weeks of my free time constructing a polyclave key⁴ where I could follow a series of identification steps that would each ~halve the number of possible mosquito species considered.

---

How’d it go?

Well, let’s give it a shot!

Here’s a mosquito, and let’s try to figure out it’s genus. We’ll start with $N$ = 48 possible genuses.

---

With the new, improved, O(log N) Polyclave Key

Step 1: On the top of it’s head, are there (A) hairs all over, (B) hairs only on the back half, or (C) no hairs at all?

Step 2: On it’s alula (kind of the armpit-ish area at the base of the wing), are there (A) broad, flat scales, (B) bristles or hairs, or (C) no scales at all?

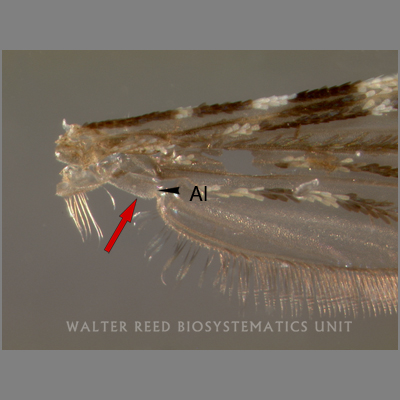
The answers, by the way, are (A) and (C), which one may have been able to eventually kinda somewhat figure out by staring hard / zoom-and-enhancing / maybe messing around with the mosquito sample to get better lighting on a tiny body part. Three more steps staring at the following areas would’ve told us that this is an Anopheles mosquito:

Each of the 5 steps had a 2 or 3 branches, so this polyclave key pretty much did in fact take the expected O(log N) steps.

---

With the Dichotomous Key

Our mosquito again, just as a reminder:

Step 1: Does it’s proboscis (a sucky tube thing emerging from where you’d think it’s mouth is) look more like (A) bent sharply downards or (B) straight?

Step 2: Does it look like it has (A) 2 fluffy “antennae” also emerging from it’s head or (B) not?

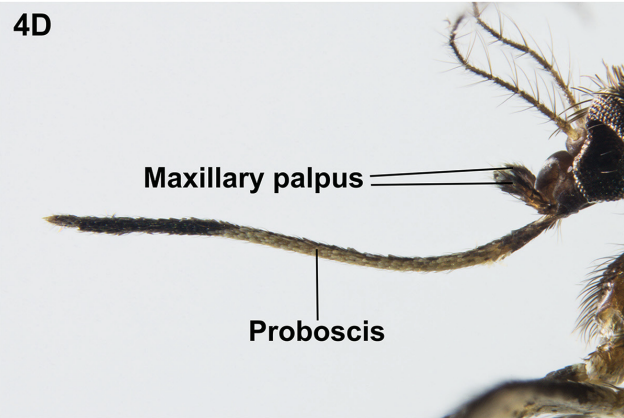
Voila! If you answered (B) and (A), which I suspect you may have been able to do without too much effort, we’re done! The key tells us that, as expected, this is an Anopheles mosquito.

---

What’s going on here???

Even though my polyclave key reduced the worst-case “number of steps” complexity to O(log N), it was actually harder and slower to use in practice. Why?

---

knowing the input distribution lets us look beyond worst-case

Firstly, it turns out that in the dichotomous keys we use, a majority of the types of mosquitoes that occur the most frequently are identified extremely early on in the key.

In other words, although the worst-case traversal might take 20+ steps, the mosquitoes that actually show up 90% of the time (e.g. Anopheles, Aedes, Culex) are classified within the first 3 or 4 identification steps.

When writing code, I’d often obsess over worst-case bounds — but if my system spends 99% of its time handling the easy cases, and only rarely hits the slow path, that’s something that could be totally acceptable depending on the situation!

Hash tables are an example of such a situation in Computer Science, and mosquito identification was definitely such a situation for me — I was happy to sacrifice pretty terrible “tail latency” because it usually meant that I’d be identifying a unique or rare species of mosquito.

For example, I once spent up to 2 hours trying to identify a single mosquito. It ended up being a Heizmannia scintillans, and the Walter Reed Biosystematics Unit’s description of the mosquito puts succinctly why it felt “worth it” to me:

Heizmannia species are amongst the most handsome of Aedines — vividly decorated with multi-colored, iridescent scales

---

constant-time steps aren’t equally cheap

Additionally, these dichotomous keys are often designed such that the earliest identification steps are the “easiest to perform”.

Something I’d learn is that not all identification steps are created equal. In theory, every step in a key might seem to take the same “amount of work” — you answer one question, move to the next. But in practice, the cost of each step could vary wildly.

Some steps were almost free: checking if a proboscis is bent or if there are 2 extended maxillary palps (our examples above!) could done with a single glance through a magnifying glass.

Others were far more tedious and error-prone: examining tiny scales on the alula meant adjusting magnification, backlighting, and painstakingly manipulating a fragile mosquito — a process that could take several minutes and risk destroying the sample.

sometimes we'd get mosquito samples that were...
pre-disfigured for us...

Similarly, a simple integer addition and a cache miss can both be “constant-time” operations in Big O, but their real-world costs differ by orders of magnitude. Traversing a pointer-rich structure (like a tree) might be “cheap” asymptotically, but involve so much pointer chasing and cache thrashing that it’s practically slower than a dense linear scan.

When optimizing algorithms, I couldn’t just count operations — but I should measure and understand the real cost behind each one.

---

think about $x_0$ before asymptotic limits

Finally, there’s the simple fact that the mosquito lab didn’t have an infinite number of species.

Our working set was around $N = 48$ genuses, and maybe a few hundred species if I went down to fine-grained identification. At this scale, asymptotic improvements barely mattered⁵.

The difference between an O(N) traversal and an O(log N) traversal might’ve saved me, at most, a handful of steps — but that was far less important than making each step easy and reliable.

When I finally took the data structures & algorithms course in university, where I actually finally paid attention, I’d learn that Big O notation only describes how algorithms behave as $N$ grows towards infinity. But in practice, every algorithm has a “crossover point” $x_0$ — a size beyond which the asymptotic behavior actually becomes the dominant thing that matters.

Before $x_0$, constants, hidden overheads, and real-world messiness — like microscope fiddling times — completely dominate performance.